This write up is a report to share our insights from learning Formal Verification and reviewing how it can be used to formally verify zk circuits.

2024-10-21 Formal Verification

What is Formal Verification

Machine assisted property verification of formal propositions.

Comparison with Informal Verification (regular math proofs):

• FV leaves no ambiguity, IV needs human interpretation
• FV is checked by machine, IV is checked by (expert) (fragile) human
• FV is very verbose and cumbersome, IV is more succint and clean

Uses of Formal Verification

Traditionally used for software programs.

Prove that:

• A program always terminates
• A program never accesses arrays out of bounds
• A program never stack overflows
• A function implementation is functionally equivalent to its spec

Also has been used for Smart Contracts. Example:

• Given any sequence of calls, the total token balance is always the same after the minting process.

Uses of Formal Verification

Can be used to verify zk circuits

Examples:

• For any inputs, the witness that satisfies the constraints is unique
• For any input, the output with a valid witness is functionally equivalent to a spec
• Given two circuits, prove that they accept the same set of inputs-ouputs
  • Note: one circuit could be the optimized version

Formal Verification approaches

Two categories of tools to do formal verification:

• Automated Theorem Provers: given a proposition, return true or false (or timeout). These are SAT solvers, SMT solvers, etc.
  • Examples: z3, cvc5
• Proof Assistants: given a proposition, manually guide the tool to build a proof.
  • Example: Lean, Isabelle, Agda, ACL2, Coq

Study Group

We made a study group and followed the “Software Foundations, Volume 1: Logical Foundations” book to learn Coq

• Book: https://softwarefoundations.cis.upenn.edu/lf-current/toc.html
• Time: 8h/week
• Members: Even, Soowon, Dohoon, Edu

Coq

• An interactive proof assistant implemented in Ocaml
• Includes a functional language (called gallina) were proofs are first class
• Propositions are encoded as (dependent) types
  • proof-checking becomes type-checking
• Means rooster in French

Practice: Basic Example

The language is very minimal and only provides a very small set of primitives. Primitive types and operations are defined via libraries.

Source of these examples is “Software Foundations, Volume 1: Logical Foundations”.

Natural numbers:

Inductive nat : Type :=
  | O
  | S (n : nat).

> A natural is 0 or next(n) Examples:

• O -> 0
• S O -> next(0) -> 1 + 0 -> 1
• S S S O -> next(next(next(0))) -> 1 + 1 + 1 + 0 -> 3

Natural addition:

Fixpoint plus (n : nat) (m : nat) : nat :=
  match n with
  | O => m
  | S n' => S (plus n' m)
  end.

> To do plus n m: > if n is 0, the result is m > if n is 1+n', the result is 1 + (plus n' m) Examples:

• plus 0 5 -> 5
• plus 2 3 -> 1 + (plus 1 3) -> 1 + 1 + (plus 0 3) -> 1 + 1 + 3 -> 5

Basic proof:

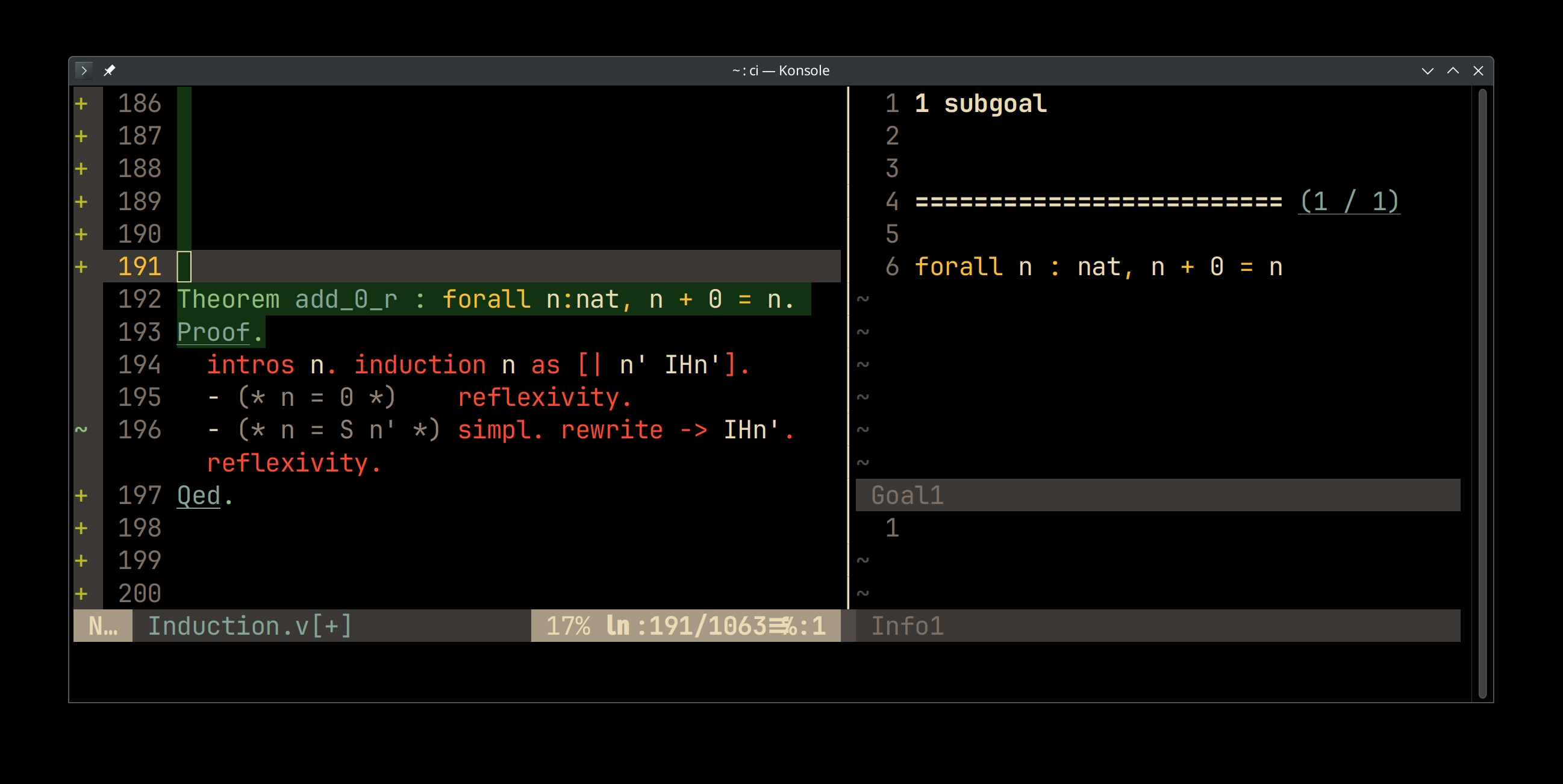
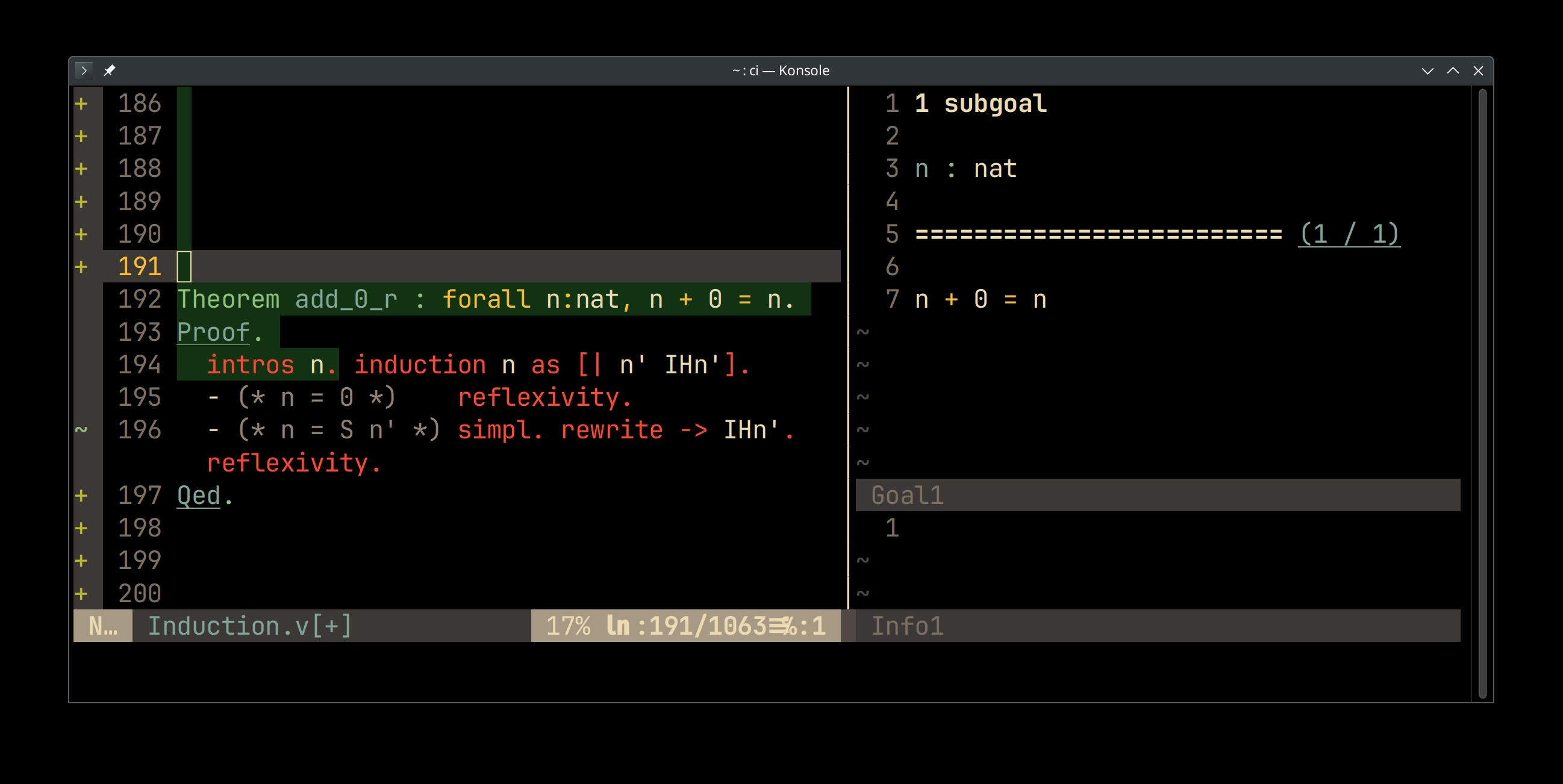
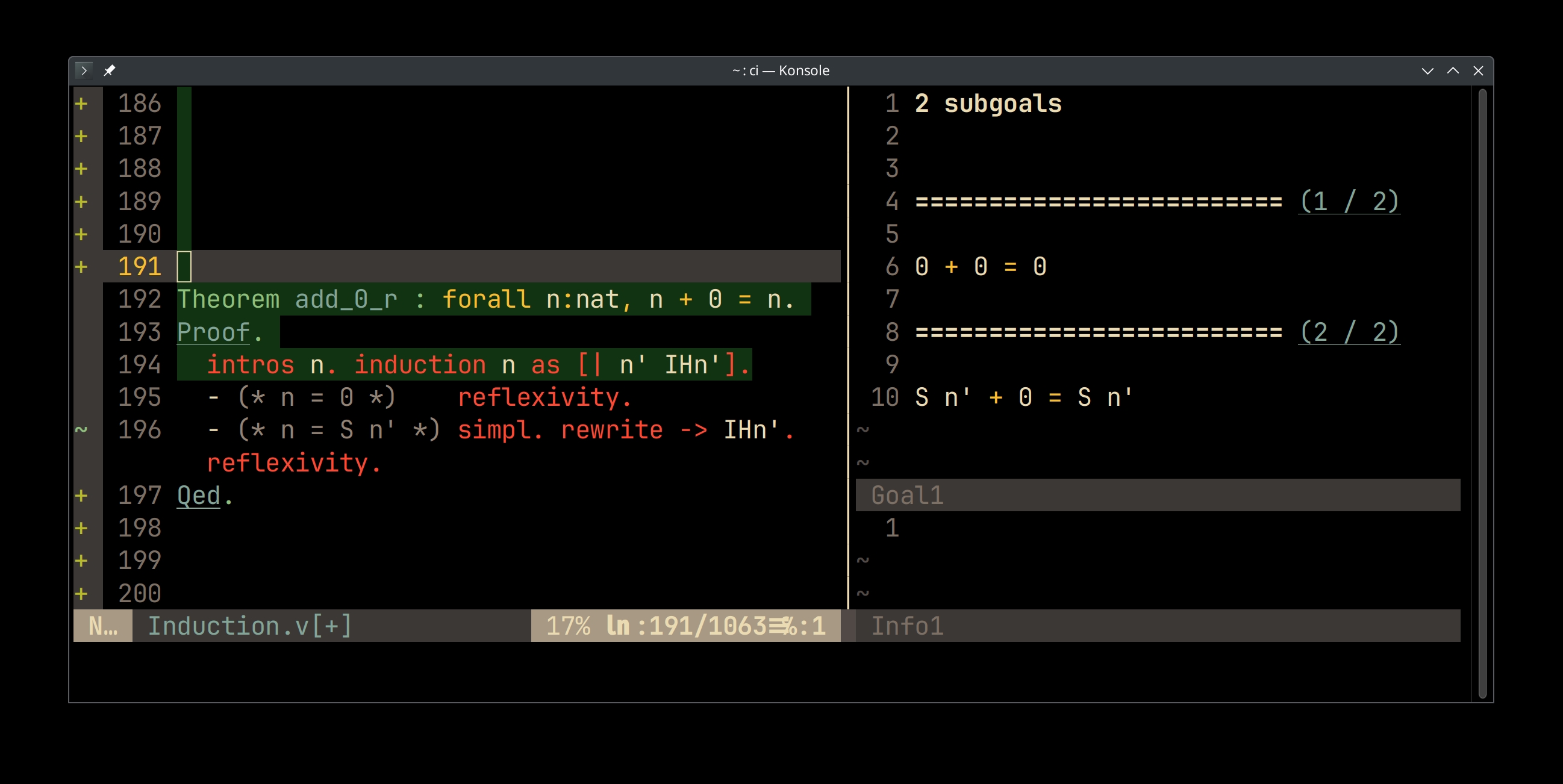
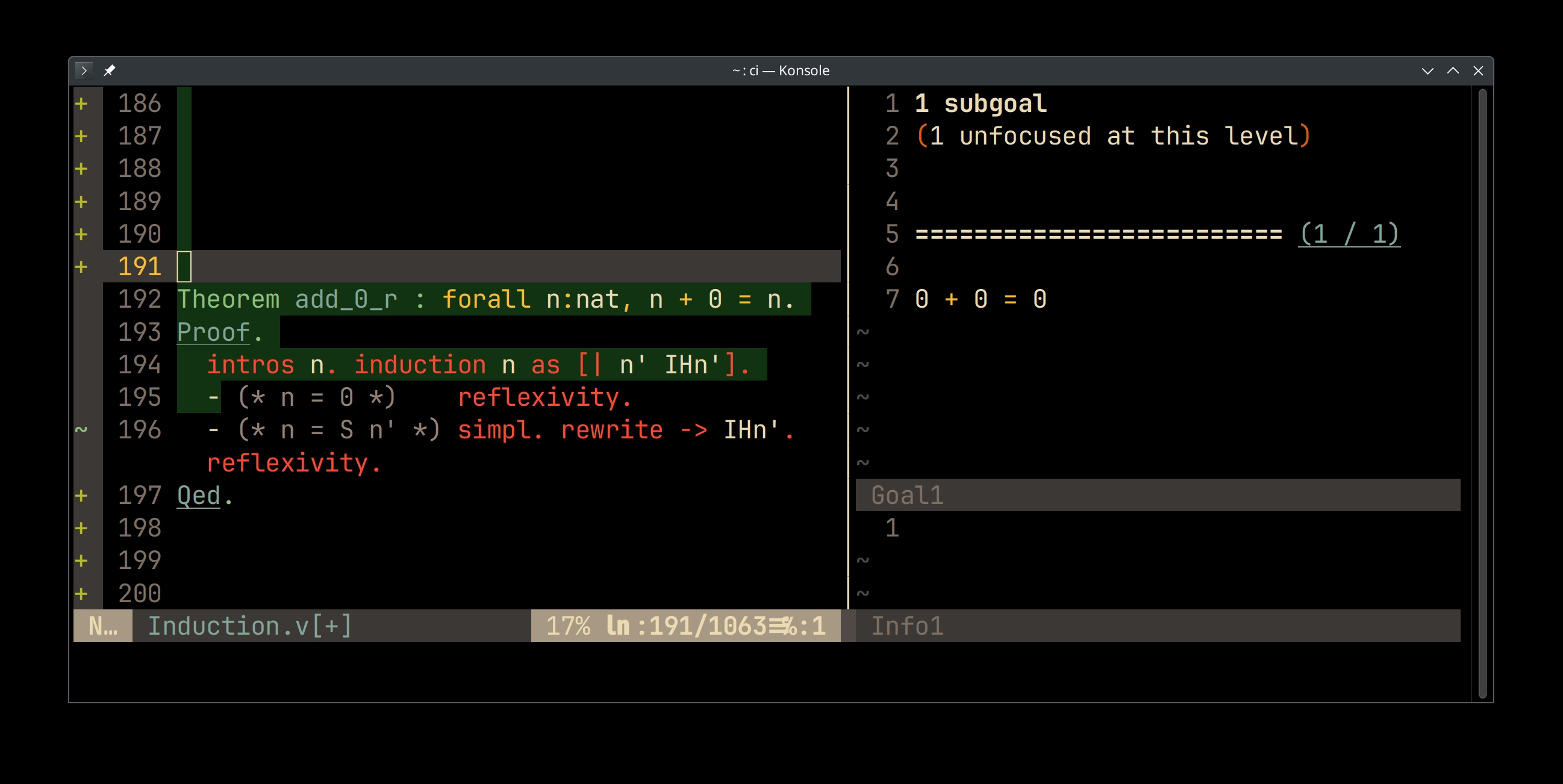
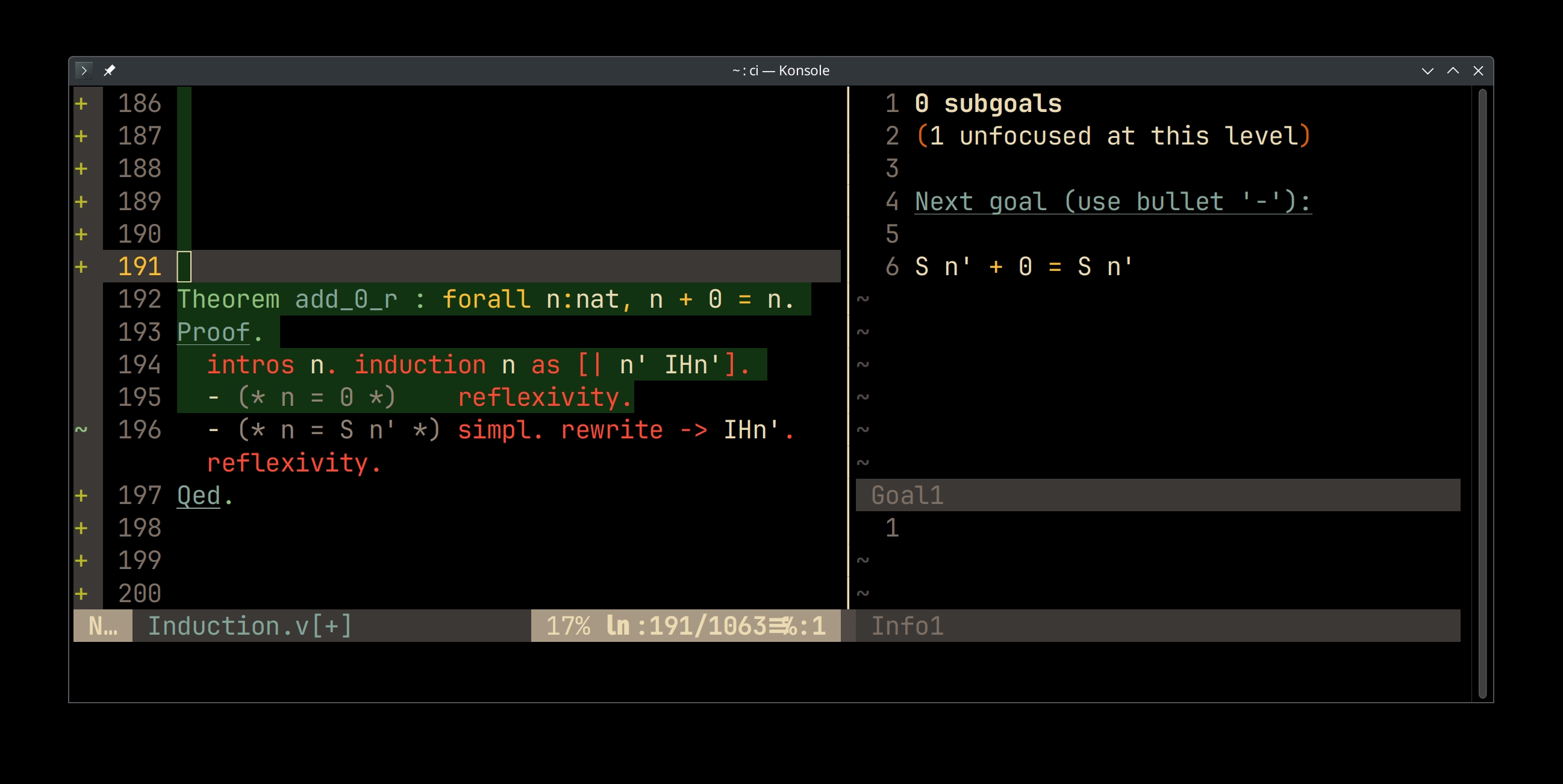
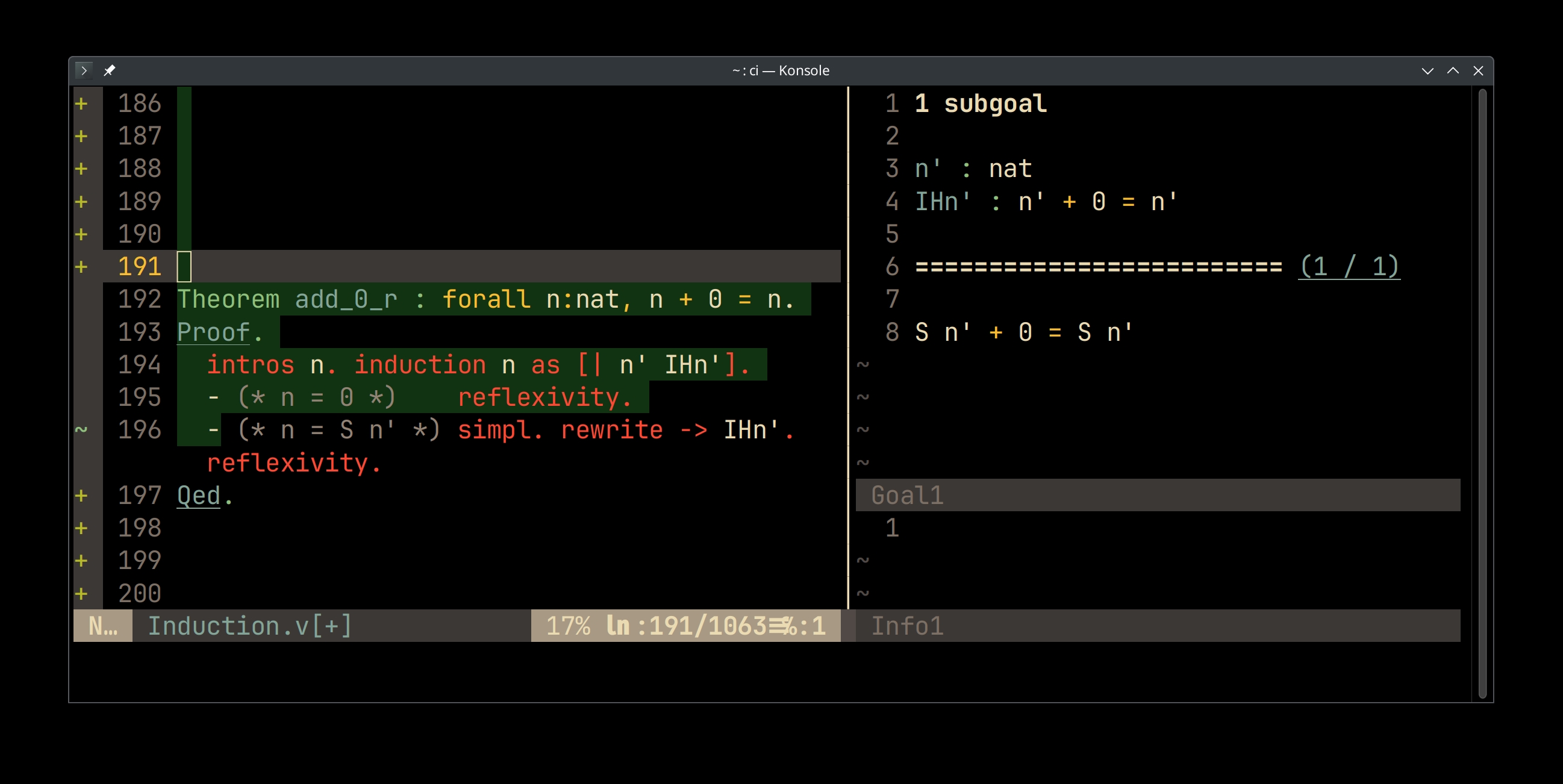
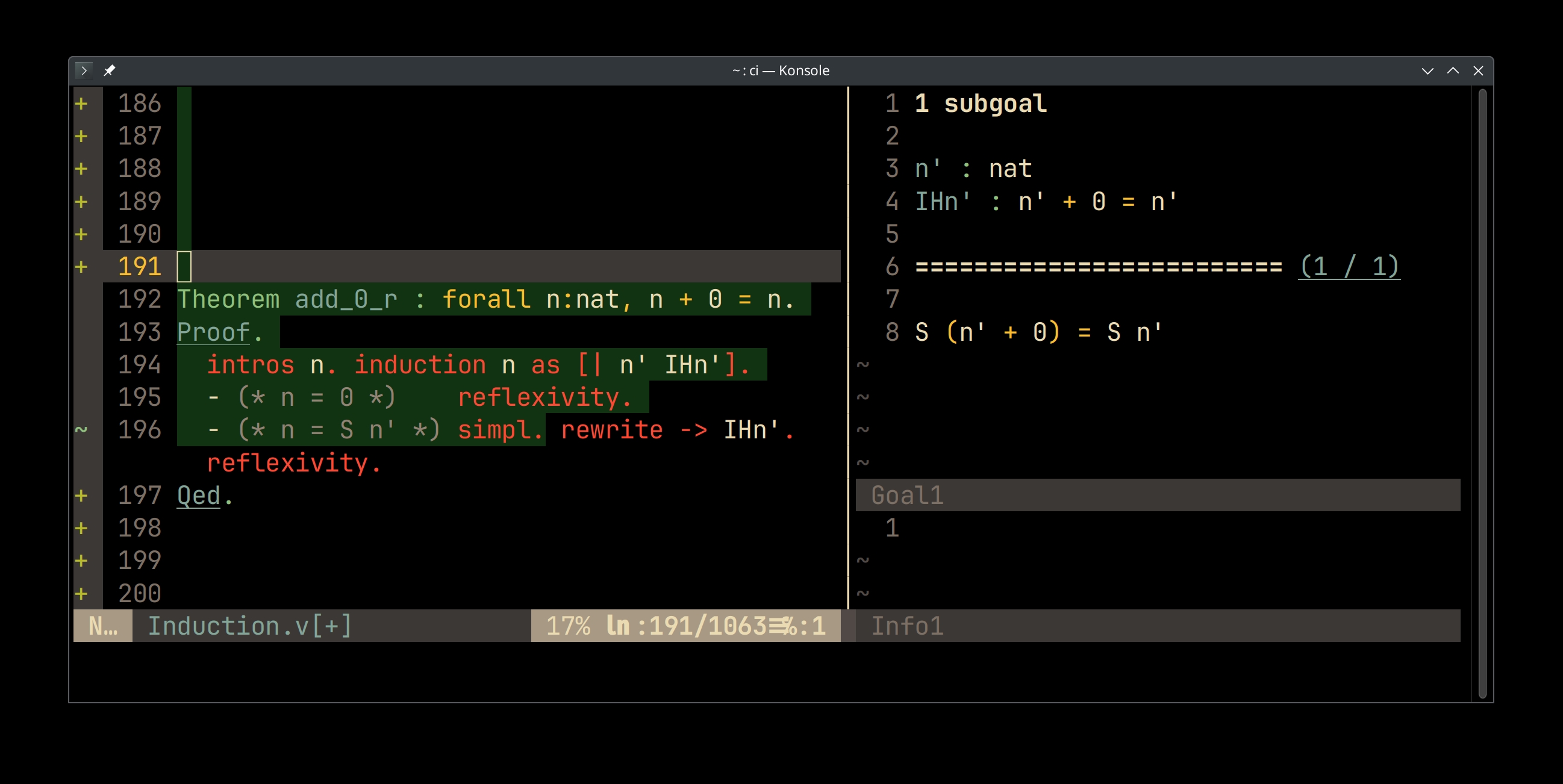
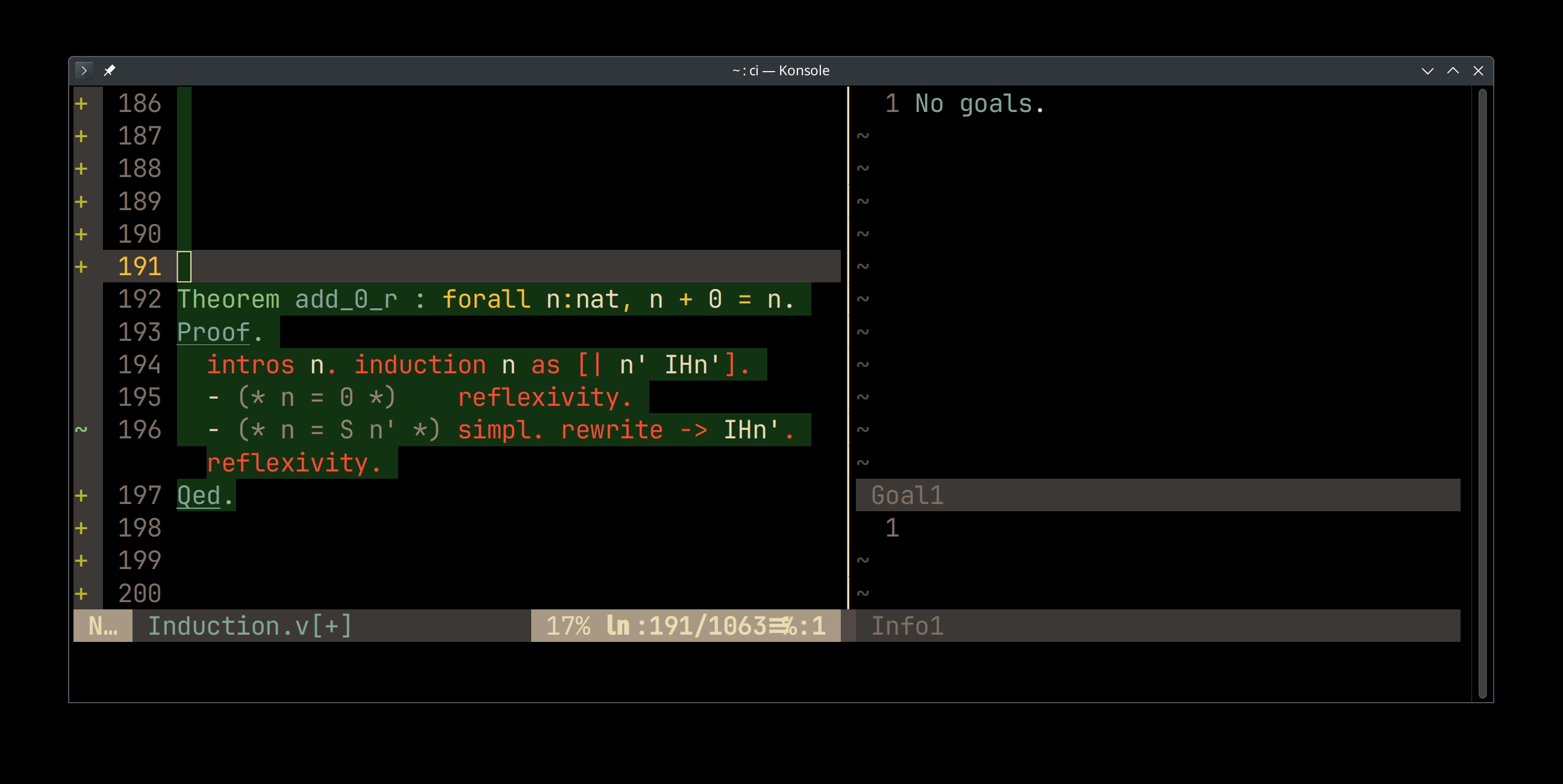
Theorem add_0_r : forall n:nat, n + 0 = n.
Proof.
  intros n. induction n as [| n' IHn'].
  - (* n = 0 *)    reflexivity.
  - (* n = S n' *) simpl. rewrite -> IHn'. reflexivity.  Qed.

> Prove that for all n, n + 0 = n > Induction by n > Base case: > - n = 0. Then we have 0 + 0 = 0. > - By definition of plus this is True. > Inductive case: > - Inductive hypothesis: n' + 0 = n' with n = 1 + n' > - We need to prove 1 + n' + 0 = 1 + n' > - Which is the same as 1 + (n' + 0) = 1 + n' > - We rewrite our goal using the hypothesis equality and get: > - 1 + n' = 1 + n' > - Which is True.

Practice: Demo

Checking the add_0_r proof interactively.

• Left pane: source code
• Right upper pane: proof status view
  • Above the separator: list of hypothesis: propositions assumed to be true
  • Below the separator: goal: proposition to prove

Theory: Classical vs. Constructive Logic

Consider the proposition $\forall P:\text{Prop},P\vee \text{[PARSE ERROR: Undefined("Command("neg")")]}P$. We know it to be true and we can use it in classical proofs:

• We don’t know if $P$ is True or not
• We prove the case $P$
• We prove the case $\text{[PARSE ERROR: Undefined("Command("neg")")]}P$
• Since each both cases cover everything, we can use it any time.
• The proposition is proven without learning the truth of $P$

But this principle can’t be derived in Coq because it follows Constructive Logic:

• We need to branch disjunctions into the True path (but here we don’t know which one it is, and can’t prove it)
• As a consequence, all Coq proofs come with an existential witness for the proof
  • In propositions that include $\exists x$, the proof will include a particular value of $x$. This is not always the case in classical proofs.

Nevertheless we can still use it as an unproven Lemma in Coq :)

Practice: Pigeonhole principle example

Informal Theorem and Proof:

> Source: MIT 18.211: COMBINATORIAL ANALYSIS, FELIX GOTTI

The same Theorem and Proof in Coq:

Lemma in_split : forall (X:Type) (x:X) (l:list X),
  In x l ->
  exists l1 l2, l = l1 ++ x :: l2.
Proof.
  intros X x l H.
  induction l as [|x' l' IHl'].
  - destruct H.
  - inversion H.
    + exists []. exists l'. simpl. rewrite H0. reflexivity.
    + apply IHl' in H0. destruct H0 as [l1 [l2 H1]].
      exists (x' :: l1). exists l2. simpl. f_equal. apply H1.
Qed.

Inductive repeats {X:Type} : list X -> Prop :=
  | Repeats   x l (H: In x l)    : repeats (x :: l)
  | RepeatsRm x l (H: repeats l) : repeats (x :: l)
.

(** Now, here's a way to formalize the pigeonhole principle.  Suppose
    list [l2] represents a list of pigeonhole labels, and list [l1]
    represents the labels assigned to a list of items.  If there are
    more items than labels, at least two items must have the same
    label -- i.e., list [l1] must contain repeats.

    This proof is much easier if you use the [excluded_middle]
    hypothesis to show that [In] is decidable, i.e., [forall x l, (In x
    l) \/ ~ (In x l)].  However, it is also possible to make the proof
    go through _without_ assuming that [In] is decidable; if you
    manage to do this, you will not need the [excluded_middle]
    hypothesis. *)

Theorem pigeonhole_principle: excluded_middle ->
  forall (X:Type) (l1  l2:list X),
  (forall x, In x l1 -> In x l2) ->
  length l2 < length l1 ->
  repeats l1.
Proof.
  intros EM X l1. induction l1 as [|x l1' IHl1'].
  - (* l1 = [] *)
    intros l2 H1 H2. destruct l2.
    + inversion H2.
    + inversion H2.
  - (* l1 = x :: l1' *)
    simpl. intros l2 Hi Hl. unfold excluded_middle in EM. destruct (EM (In x l1')).
    + (* [In x l1'] means that the repeated element in [l1] is [x] *)
      apply Repeats. apply H.
    + (* [~ In x l1'] means that the repeated element in [l1] is not [x] *)
      apply RepeatsRm. assert (Hix : In x l2). { apply Hi. left. reflexivity. }
      apply in_split in Hix. destruct Hix as [l21 [l22 El2]].
      apply (IHl1' (l21 ++ l22)).
      * intros x0 Hix0.
        assert (Hix02 : In x0 l2). { apply Hi. right. apply Hix0. }
        rewrite El2 in Hix02. rewrite In_app_iff in Hix02. rewrite In_app_iff.
        destruct Hix02 as [Hix0l21 | Hix0l22].
        ** left. apply Hix0l21.
        ** right. simpl in Hix0l22. destruct Hix0l22.
          *** rewrite H0 in *. destruct (H Hix0).
          *** apply H0.
      * unfold lt in *. apply le_trans with (length l2).
        ** rewrite app_length. rewrite El2. rewrite app_length. simpl. 
          rewrite plus_n_Sm. apply le_n.
        ** apply Sn_le_Sm__n_le_m. apply Hl.
Qed.

> Source: Software Foundations exercise solution by Soowon. I wasn’t able to complete this one :(

Theory: verifying zk circuits

> Source: > Compositional Formal Verification of Zero-Knowledge Circuits > by Alessandro Coglio and Eric McCarthy and Eric Smith and Collin Chin and Pranav Gaddamadugu and Michel Dellepere > Cryptology {ePrint} Archive, Paper 2023/1278 > https://eprint.iacr.org/2023/1278.pdf

• Soundness: Any input-output that can pass the constraints (with some witness) is valid (according to the spec function)
• Completeness: Any valid input-output (according to the spec function) can pass the constraints (with some witness)
• Correctness: Soundness and Completeness

Practice: circomlib’s IsZero proof

Source code from Veriside/Coda circomlib Formal Verification project: https://github.com/Veridise/Coda/blob/96e5c94e1a27d25466f24beee31c010810273e33/BigInt/src/CircomLib/Comparators.v#L38

Original circom:

template IsZero() {
    signal input in;
    signal output out;

    signal inv;

    inv <-- in!=0 ? 1/in : 0;

    out <== -in*inv +1;
    in*out === 0;
}

Extracted constraints:

Definition cons (_in out: F) :=
  exists _inv,
  out = 1 - _in * _inv /\
  _in * out = 0.

> Exists inv such that > out = 1 - in * inv AND > in * out = 0

Manually written spec:

Record t : Type := { _in: F; out: F; _cons: cons _in out }.

Definition spec (c: t) : Prop :=
  if (c.(_in) = 0)? then
    c.(out) = 1
  else
    c.(out) = 0.

> If in == 0 then out = 1 else out = 0

Soundness proof:

Theorem soundness:
  forall (c: t), spec c.
Proof.
  unwrap_C.
  intros. destruct c as [x y [x_inv H]].
  unfold spec, cons in *. simpl.
  intuition.
  destruct (dec (x = 0)); fqsatz.
Qed.

> Prove that for all input-output pairs that follow the constraints, the spec is satisfied. > The proof involves proving the case where in = 0 and in != 0.

Not all components are as easy to prove; take a look at the soundness proof of LessThan: https://github.com/Veridise/Coda/blob/96e5c94e1a27d25466f24beee31c010810273e33/BigInt/src/CircomLib/Comparators.v#L161

Some open challenges

• How to model and prove lookups?
• How to model and prove permutation checks?
• How to model and prove random challenges in the circuit (Fiat-Shamir heuristic)?

Next steps

We have learned how to write formal proofs with Coq.

We have an intuition of how to use Coq to verify zk circuits.

The next (reasonable) step would be to formally verify an existing PSE project.

• This would be a full-time project
• Would include subtasks like tool building:
  • Coq libraries to work with field arithmetic expressions
  • Arithmetization extractors for a particular zk framework
• We probably will not do it now because the team members plan to focus on other projects.
• Link with resources for next steps: https://hackmd.io/o0Jxi_SbQwOQUCwpELTwEQ?view